A classe de matemàtiques hem estat treballant en un nou projecte. Ens van presentar un problema sobre els poliedres regulars, el qual vam haver de resoldre en grups.
Els poliedres regulars són aquells poliedres que les seves cares són polígons regulars i té tots els costats i angles iguals. El cub, l'octaedre, el dodecaedre, el tetraedre i l'icosaedre són els cinc poliedres regulars.
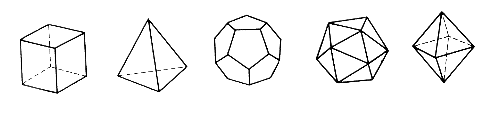
El problema consistia en, completar una taula sobre els poliedres regulars amb les dades següents:
1: Les seves cares.
2: Els seus vèrtex.
3: Les seves arestes.
Quan ja vam tenir les figures muntades, vam comptar les seves arestes i els seus vèrtex i vam completar la taula.
Un cop vam tenir totes les dades, la professora ens va proposar un repte, descobrir quin era el Teorema d’Euler. Aquest teorema indica quina és la relació entre cares, vèrtex i arestes que es compleix sempre en un poliedre regular.
Un cop vam tenir totes les dades, la professora ens va proposar un repte, descobrir quin era el Teorema d’Euler. Aquest teorema indica quina és la relació entre cares, vèrtex i arestes que es compleix sempre en un poliedre regular.
Desprès de reflexionar i parlar molt amb el grup, vam descobrir que si sumes les cares d’un poliedre regular, més els seus vèrtex sempre dóna de resultat el nombre d'arestes més 2.
Aquest teorema es pot expressar de diferents maneres però totes indiquen el mateix.
La nostra conclusió és que el Teorema d’Euler és igual a:
C+V-2= A
C+V= A+2
A-V= C-2
Anem a comprovar-ho:
Un cub té 6 cares, 12 arestes i 8 vèrtex.
C+V-2= A C+V= A+2 A-V= C-2
Anem a comprovar-ho:
Un cub té 6 cares, 12 arestes i 8 vèrtex.
C+V-2= A C+V= A+2 A-V= C-2
6+8-2= 12 6+8= 12+2 12-8= 6-2

Cap comentari:
Publica un comentari a l'entrada